Una regla para medir el universo.

«La siguiente exposición referente a los periodos de veinticinco variables en la Pequeña Nube de Magallanes fue preparada por Miss Leavitt» (Pickering, Charles. Harvard College Observatory. Circular 173)

Así de alegre comenzaba la circular 173 del Harvard College Observatory publicada en 1912 y firmada íntegramente por su director, Edward Charles Pickering. Desconocemos por qué Henrietta Swan Leavitt no firmó este trabajo, continuación directa del que publicó en 1908, pero sí podemos afirmar que pocas veces en la historia de la ciencia un artículo de apenas tres páginas ha resultado tan rentable para el conocimiento humano.

Circular firmada por Pickering y "preparada" por Henrietta

Estas variables son cefeidas, pero aún no lo sabemos.

«Recuerdan a las variables encontradas en los cúmulos globulares, que disminuyen lentamente su brillo, permaneciendo cerca del mínimo una gran parte del tiempo, e incrementándolo muy rápidamente hasta un breve máximo» (Pickering, Charles. Harvard College Observatory. Circular 173).

De las miles de estrellas variables que descubrió en las Nubes de Magallanes, Henrietta había seleccionado en su artículo anterior un puñado de ellas con unas características muy peculiares. Este grupo, junto a ocho nuevas variables, conformaba las veinticinco estrellas protagonistas de este nuevo trabajo de la calculista de Harvard.

En realidad, este tipo de estrella variable ya era conocido. En esa misma década, Solon Bailey, astrónomo de Harvard que terminaría dirigiendo el Observatorio tras la muerte de Pickering, había descubierto un tipo de estrella variable muy similar en asociaciones estelares muy pobladas y viejas, denominadas cúmulos globulares.

Pero tampoco Bailey fue el primero que las observó. Más de un siglo antes, en 1784, el astrónomo amateur, John Goodricke había descubierto un comportamiento idéntico en la estrella Delta Cephei de la constelación de Cefeo. Precisamente en su honor, este tipo de estrellas variables recibe el nombre de Cefeidas (aunque, paradójicamente, la primera cefeida observada no fue Delta Cephei, sino la estrella Eta Aquilae, descubierta unos meses antes por Edward Piggot, astrónomo y vecino de Goodricke).

J.Goodricke, el "casi" descubridor de las cefeidas.

En la historia de la astronomía el nombre de Henrietta S. Leavitt está inevitablemente ligado a este tipo de estrellas variables, pero curiosamente la palabra cefeida no se menciona ni una sola vez en todo el artículo. No fue hasta años después que la comunidad astronómica comenzó a emplear este término para referirse a las estrellas de Henrietta.

Las cefeidas son estrellas de entre cuatro y veinte veces la masa del Sol, con periodos muy regulares que suelen estar comprendidos entre unas pocas horas a meses. Durante un ciclo de variabilidad estas estrellas pueden aumentar hasta cuatro veces su brillo.  Además, como cita Henrietta en el artículo, su curva de luz suele ser, en la mayoría de los casos, asimétrica, con un rápido ascenso hacia la luminosidad máxima y un descenso más lento hacia la mínima.

Curvas de luz de estrellas cefeida

Pero lo que llamó la atención de Henrietta de estas estrellas no fue tanto su curva de luz como la evidencia de que existía una relación directa entre su periodo de variabilidad y su brillo en el cielo. Y de esto es de lo que realmente va el artículo de Henrietta..., perdón, queríamos decir de Pickering.

Más brillantes, periodos más largos.

«[…]las variables más brillantes tienen también los periodos más largos[…]» (Pickering, Charles. Harvard College Observatory. Circular 173)

Henrietta descubrió que las cefeidas aparentemente más brillantes de la Pequeña Nube de Magallanes pulsaban más lentamente y, por el contrario, las menos brillantes lo hacían con un periodo más corto. Esta relación entre el periodo y el brillo fue representada gráficamente por la astrónoma en el artículo. En la figura de la derecha se puede ver que la práctica totalidad de las estrellas observadas se ajustaba perfectamente a una relación lineal entre la magnitud aparente y el logaritmo de su periodo de pulsación. Cada línea de la gráfica correspondía a los valores de magnitud aparente de la cefeida en el máximo y en el mínimo de su curva de luz.

Gráficas originales del artículo de Henrietta S. Leavitt. En las ordenadas la magnitud aparente de las veinticinco cefeidas estudiadas. En la abcisa sus periodos. En la segunda gráfica el periodo es expresado en logaritmo. La curva superior corresponde al máximo de la curva de luz, y la otra al mínimo.

Esta relación, interesante por si misma, escondía una potente regla, una regla para medir el universo.

Una regla para medir el universo (pero sin unidades)

«Como las variables están probablemente a la misma distancia de la Tierra, sus periodos estarán asociados con su actual emisión de luz que dependerá de su masa, densidad y brillo superficial» (Pickering, Charles. Harvard College Observatory. Circular 173)

Las gráficas de Henrietta mostraban la relación entre el periodo de las cefeidas de la Pequeña Nubes de Magallanes y su magnitud aparente obtenida a través del análisis de las placas fotográficas. El brillo aparente de una estrella en el cielo depende de dos factores: de la distancia a la que se encuentre –cuanto más lejana, más tenue-  y de su luminosidad, es decir, de la cantidad de energía que emite por unidad de tiempo. Por otro lado, el periodo de pulsación de una cefeida debe ser algo intrínseco a la propia estrella, así que no depende de la distancia a la que esta se encuentre de nosotros. Decir lo contrario sería como asegurar que el color de pelo de alguien varía según lo lejos o cerca que se halle. Por lo tanto, en realidad, la ley de Henrietta esconde una íntima relación entre el periodo de una cefeida y su luminosidad: si una cefeida tiene un periodo de pulsación mayor es porque realmente es más luminosa que otra que pulse en un tiempo más corto, independientemente de la distancia a la que se encuentre cada cual. Esto es un hecho trascendente ya que, salvo casos excepcionales, no podemos conocer la luminosidad de una estrella de manera directa, pero sí su periodo de pulsación. De hecho, Henrietta no conocía la luminosidad de sus cefeidas, y sus tablas y gráficas solo contenían la magnitud aparente de estas.

Pero, como la propia calculista destaca en su texto, la Pequeña Nube de Magallanes es un asociación estelar, y por lo tanto todas sus estrellas, incluidas las cefeidas,  debían estar aproximadamente a la misma distancia de la Tierra. Esta es una observación importante porque las diferencias en magnitud aparente dentro de un grupo de estrellas situadas a la misma distancia de nosotros serán exclusivamente debidas a las diferencias en la luminosidad intrínseca de cada una de ellas. Por lo tanto, Henrietta podía asegurar con absoluta certeza no solo que las cefeidas que aparecían en la gráfica como las más brillante eran realmente las más brillantes y al contrario, sino que además las diferencias de magnitud entre ellas eran directamente traducibles a diferencias en luminosidad. Bastaría, por tanto, conocer la luminosidad de una sola de estas cefeidas para poder calibrar toda la gráfica en magnitudes absolutas –la unidad empleada en astronomía para medir luminosidad- y obtener así la auténtica relación periodo-luminosidad. Pero a Henrietta esto le era del todo imposible, ya que para ello necesitaba un dato absolutamente desconocido en aquella época: la distancia a una cefeida, y no necesariamente a una de la Pequeña Nube de Magallanes.

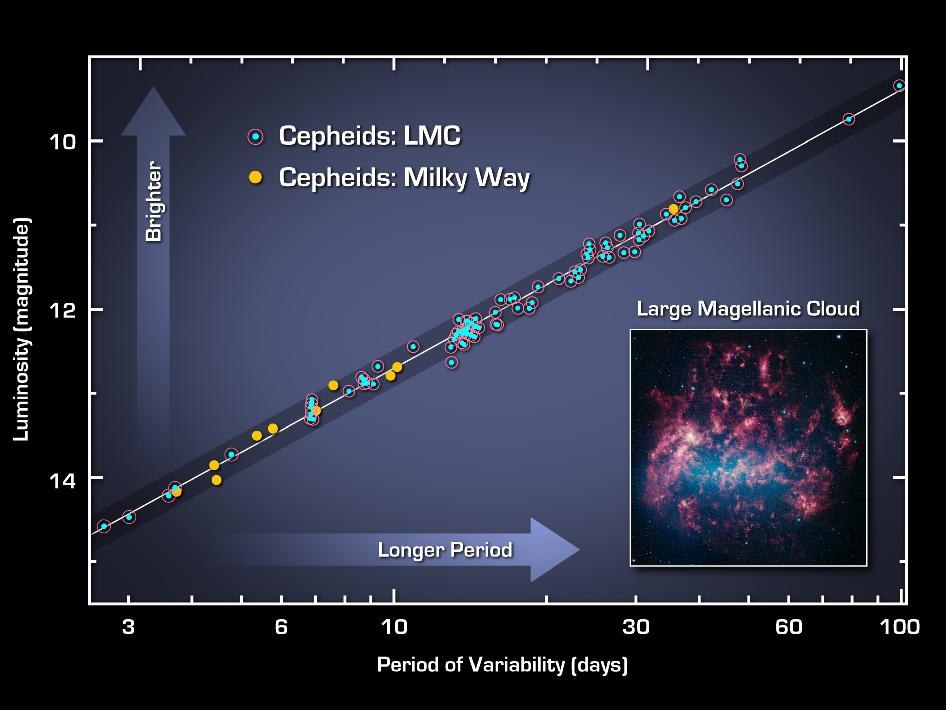
Relación periodo-luminosidad calibrada

Ley inversa del cuadrado de la distancia

La relación entre brillo aparente, luminosidad y distancia a la que se encuentra una estrella responde a la llamada ley de la inversa del cuadrado de la distancia, que  nos viene a decir que el brillo aparente de una estrella disminuye con el cuadrado de la distancia a nosotros.  Desde un punto de vista matemático e introduciendo las definiciones de magnitud, la relación entre magnitud aparente, magnitud absoluta y distancia viene dada por lo que se conoce como módulo de distancias:

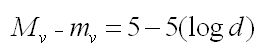
Por lo tanto, observado el brillo de un objeto en el cielo y conocida su luminosidad, se puede obtener fácilmente la distancia a la que se encuentra dicho objeto. Ya hemos comentado que desgraciadamente no es nada fácil obtener la magnitud absoluta de una estrella, excepto en el caso de que esta sea una cefeida. En este caso, podemos observar su periodo de pulsación y, empleando la ley de Henrietta, obtener su magnitud absoluta y de aquí su distancia. Pero para ello la relación periodo-luminosidad debe estar previamente calibrada.

Retomando el hilo de nuestra historia, si tras la publicación del artículo de la señorita Leavitt alguien hubiera determinado mediante otro método la distancia a una o a un grupo de cefeidas, así como su brillo aparente, podría haber determinado su magnitud absoluta empleando la formula del módulo de distancias. Con este dato y con el valor del periodo obtenido de su curva de luz podría haber calibrado en magnitudes absolutas la relación periodo-luminosidad de Henrietta. Pues bien, esto fue exactamente lo que hizo el astrónomo Ejnar Hertzsprung.

Hertzsprung, mediante una técnica astronómica conocida como paralaje estadística, infirió la distancia a cefeidas cercanas y descubrió que la magnitud absoluta de las cefeidas con un periodo de 6,6 días era exactamente de M=-2,3, es decir, más de seiscientas veces la luminosidad del Sol. Con este dato calibró en  luminosidad la gráfica de Henrietta y obtuvo que la Pequeña Nube de Magallanes estaba a treinta y tres mil años luz, una distancia absurdamente extraordinaria para aquella época (en realidad está mucho más lejos).

Ejnar Hertzsprung, el gran calibrador

En los años posteriores al trabajo de Hertzsprung se desarrollaron nuevos métodos que permitieron calibrar la relación periodo-luminosidad con mayor exactitud. El proceso era ahora relativamente sencillo. Bastaba encontrar una cefeida en algún punto del universo; estudiar su curva de luz y determinar su periodo de pulsación; introducir este valor en la ley de Henrietta correctamente calibrada y obtener su magnitud absoluta; comparar este valor con la magnitud aparente de la estrella obtenida de la observación directa y calcular la distancia a dicha estrella mediante el módulo de distancias.

Sí, esta fue la gran aportación de Henrietta y sus tres páginas de artículo: un método para determinar distancias a estrellas variables tipo cefeida. No parece gran cosa, ¿verdad? Pues tras este descubrimiento nuestro universo no volvió a ser el mismo.